誰でも英検4級【第2話】まず本試験よりはじめよ!
前回はこの「親子で英検4級合格プロジェクト」を立ち上げたきっかけについてお話ししました。
▼参考記事:親子で英検4級合格するプロジェクト【第1話】教育費を減らす方法
本試験まであと2ヶ月たらず。
さっそく勉強をはじめることにしましょう!
最初に「過去の本試験」を解くべき3つの理由とは?
2021年11月21日。
自宅にて1時間目をスタート!
まずは、過去問の問題集を購入して、子どもに最新の過去本試験(4級)を解いてもらいました。
この目的は次の3つです。
- 「今の自分」がどれくらい解けるかを確かめる。
- 本試験のレベルを確かめる。
- 自分の弱みと強みを知る。
少しこれらの目的を掘り下げて解説します。
とにもかくにも、ゴール地点から逆算することが大事です。
1)「今の自分」がどれくらい解けるかを確認!
実際に本試験を解いてもらったのは「自分」と「敵」を知るためです。
つまり、「我が子がどの程度の英語レベルか?(=「自分」)」そして「受験することになる本試験(=「敵」)がどれくらいの難易度か」を知ることが目的なのです。
これはできるだけ早めに体感することが重要!
実際に解いてみることによって「今の自分」がどれくらいテストに対応できるのかを体感するのです。
ポイントは「今の自分」というところです。
もし今全然できなかったとしても問題はありません。
いま解けなければむしろ伸びしろがありますし、今後どこを重点的に学習すればいいのか計画を立てることができます。
2)本試験のレベルも確かめよう!
本試験と同じ時間(35分)をはかって過去問を解答してもらいました。当然のことながら、この制限時間では全ての問題を回答することはできません。
そして、我が子の感想としては「かなり難しかった」とのことです。
そりゃそうだ!
最初から分かったら神童中の神童です。
本人の中で本試験のレベルがわかるとゴールが可視化されます。
そして、「あと何日でこの程度まで達成すればいいのか」という目安ができます。
これが「ゴールからの逆算」となります。
難しい言葉で表現すると「演繹法」に近いでしょうか。
目的地からさかのぼって現時点でやるべきことを認識する手法ですね。
また、英検4級からは長文読解の問題が入ってきます。
長文読解の問題は本来、「英語の総合力」が必要となるのですが、意外にも単語の推測力があるとなんとなく読めてしまいます。私の娘もこの推測力があるため、単語力や読解力がそれほどなくても正解することができるようです。
ちょっと話はそれますが、日本社会では空気を読むことがものすごく重要なので、行間を読める推察力は超貴重な能力ですよね……
ちなみに私はこの能力に自信がありません!
3)自分の弱みと強みを知ろう。
本試験を解くことによって、自分の弱みと強みを知ることができます。
そして弱点を知ることによって今後の勉強方針を固めていけます。
ちなみに、以下は私の娘のケースです。
全体的に点数はそこそこ取れていたのですが、3番の「並び替え問題」が弱い傾向にあります。
つまり、「文法の基礎の基礎」から始めた方がよいことに気づきました。
なんとなく雰囲気で問題を解いている様子だったので、自信をつけさせると同時に学習意欲をわかせる工夫が必要だとも思いました。
もちろん、強みも発見しました。
先述したように、推測力がとても高いということです。
多少の単語がわからなくても、前後の文脈からどういう内容か把握できるのです。
これは素晴らしい能力なので今後の人生にも活かせますね。すばらしい!
最後に「レーダーチャート」で実力を把握しよう!
答え合わせが終わったら、正解数をグラフ化しましょう。
これによって、どのユニットが得意かを一目で見ることができます。
(↓こんな感じです)
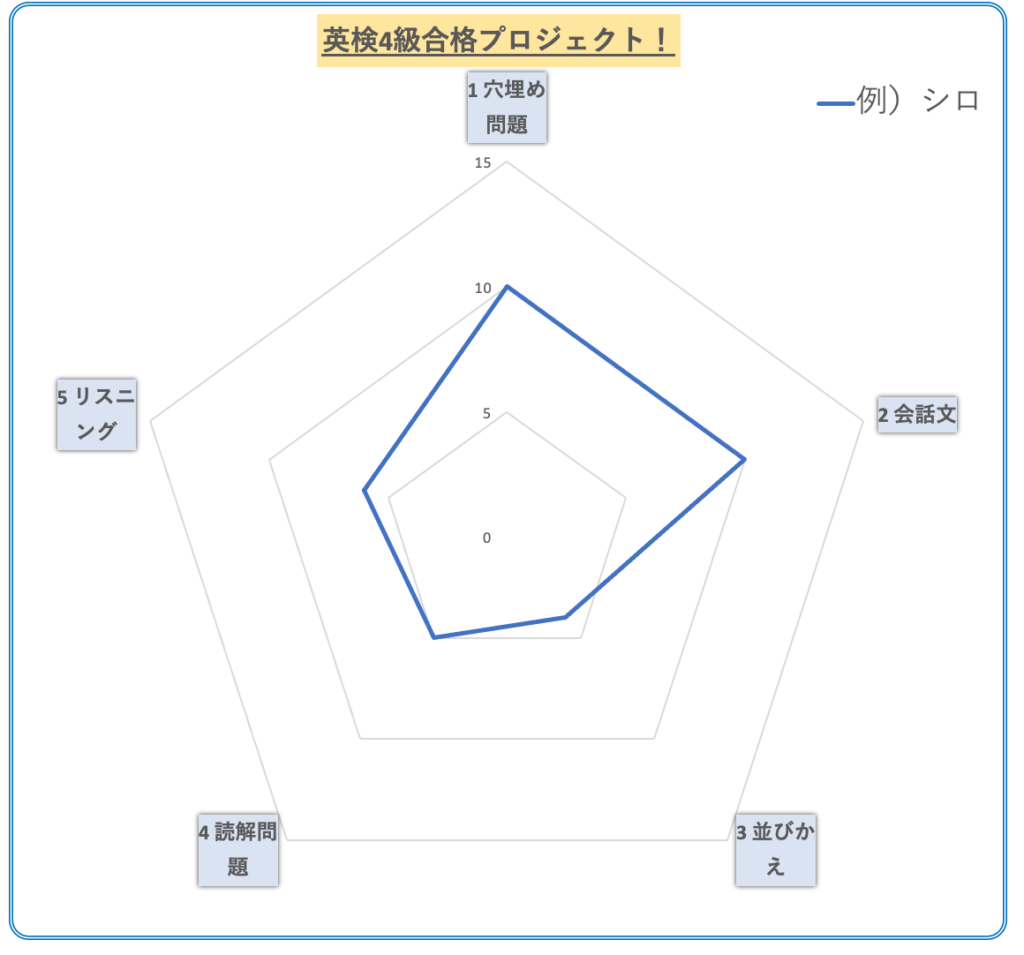
これは、いわゆる「レーダーチャートグラフ」と呼ばれるもので、一目で自分の特徴を把握できるメリットがあります。Excelのグラフ機能でかんたんに作成できます。
このレーダーチャートはすごく有効なので、後日に詳しく説明したいと思います!
次回は難関である「リスニング問題」に着手しましょう!
この記事を書いたのは私です

-
1級ファイナンシャルプランナー、宅地建物取引士。
【経歴】1977年兵庫県生まれ。一橋大学経済学部卒業後、多種の業界で管理部門をほぼ経験しました!(IT、経理、経営企画、財務、人事、マーケティング)
【得意分野】人生設計やプラン作成、分かりやすく説明したいです。
【趣味】カフェめぐり(日本全国のスタバ旅など)グルメ、ストイックな勉強。
最新の投稿
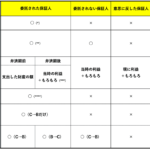 行政書士2024年10月10日行政書士直前期にチェックするべき民法「保証おまとめ表」【重要度★★】
行政書士2024年10月10日行政書士直前期にチェックするべき民法「保証おまとめ表」【重要度★★】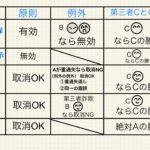 宅建士2024年10月1日【宅建士&行政書士直前期】本試験前日までにおぼえるべき「意思表示おまとめ表」【重要度★★★★】
宅建士2024年10月1日【宅建士&行政書士直前期】本試験前日までにおぼえるべき「意思表示おまとめ表」【重要度★★★★】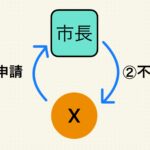 行政書士2024年9月20日【行政書士で意外と混乱するテーマ】「義務付けか?差し止めか?」問題
行政書士2024年9月20日【行政書士で意外と混乱するテーマ】「義務付けか?差し止めか?」問題 勉強!2024年9月14日【2024年】行政書士2年目の模試戦略を考えたので公表します。
勉強!2024年9月14日【2024年】行政書士2年目の模試戦略を考えたので公表します。
